Reduce costs with disk-based vector search
Vector search has gained significant attention in the area of information retrieval thanks to advances in natural language embedding models. These models map domain-specific data into a vector space, where similar pieces of data are positioned close to each other. When you run a search, the query is embedded into this space, and a nearest neighbor search identifies the most similar results based on distance calculations.
Vectors are arrays of fixed dimensions that store numeric values (float, byte, or bit). The shape of the vector and the function used to compare vectors are determined by the embedding model. For example, when you pass a chunk of text to the Cohere v3 multilingual embedding model, the model returns a 1,024-dimensional vector of 32-bit floating-point numbers representing the text in the vector space, as shown in the following image.
To determine similarity, the “distance” between vectors is computed using functions like the dot product or the Euclidean metric. The choice of distance function is typically dictated by the model that generates the embeddings. Vector search excels at capturing the implicit meaning of data, often leading to more accurate results. Additionally, combining vector search with traditional text-based search can further improve search quality.
The memory footprint of vector search
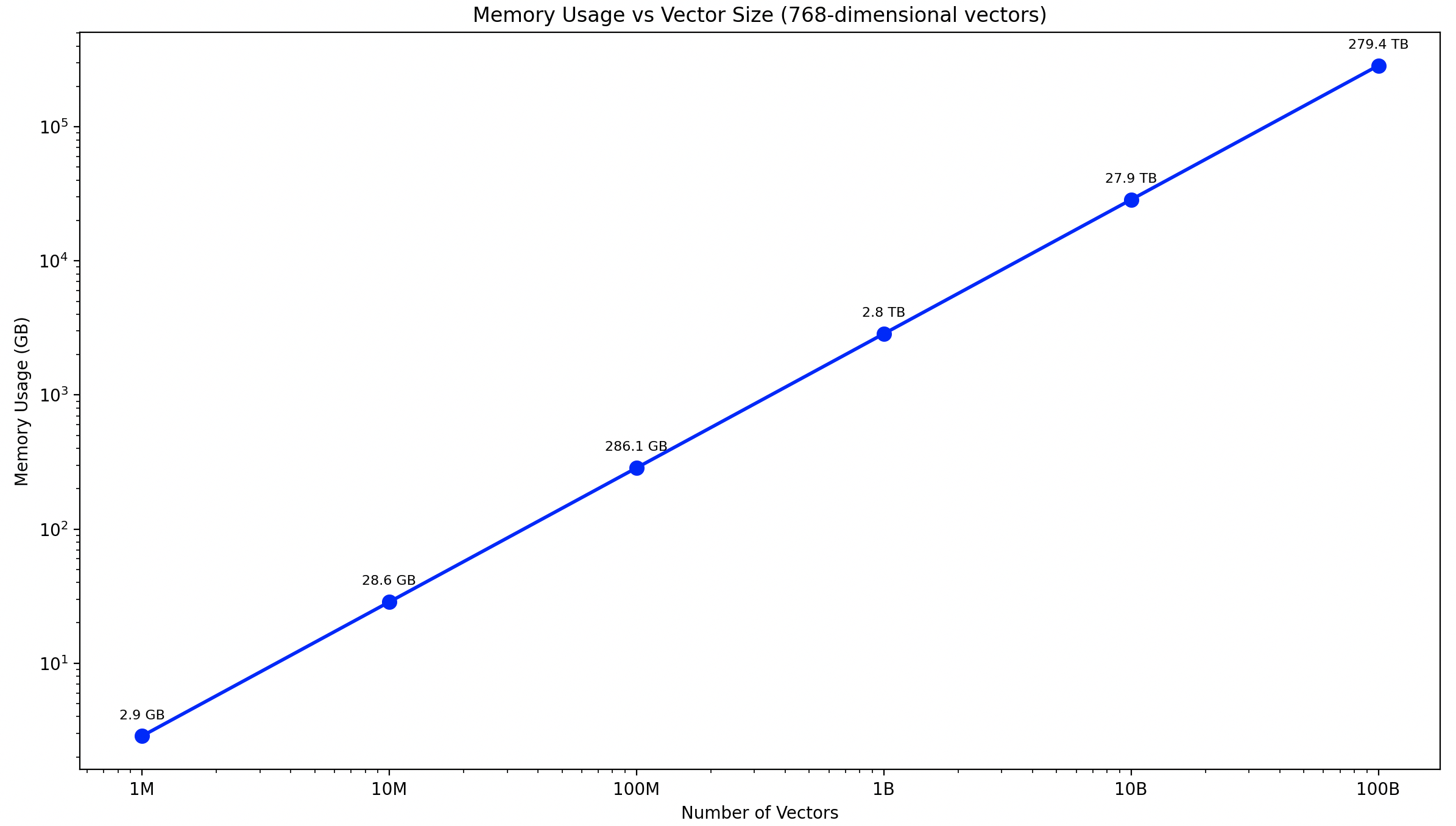
Vector-based indexes can be very large. For example, storing 1 billion 768-dimensional floating-point embeddings requires approximately 1000^3 * 768 * 4 ~= 2861 GB of storage. This cost increases further when replicas are enabled and additional metadata is added. Traditionally, many efficient nearest neighbor algorithms require vectors to be fully resident in memory to enable fast search because search involves random access patterns. This makes it difficult to efficiently retrieve vectors from disk and leads to high costs as the number of vectors increases, as shown in the following figure.
To reduce the memory footprint of vector indexes, vector quantization techniques are typically employed. Quantization compresses vectors into smaller representations while trying to minimize information loss. For example, FP16 quantization converts 32-bit floats to 16-bit floats, reducing memory usage by half. Because many datasets do not require the full 32-bit space, we do not commonly see a reduction in accuracy with this approach.
In addition to FP16, quantization can be used to compress vectors even further, with compression factors of 4x, 8x, 16x, 32x, and beyond. Reducing memory usage further translates to significant cost savings.
However, quantization comes with a trade-off: The more compression that is applied, the greater the potential reduction in search accuracy. Fortunately, with improvements in secondary storage, it’s possible to trade some search latency for accurate nearest neighbor search in a low-memory environment.
Disk-based vector search in OpenSearch
In 2.17, we introduced an on_disk mode for knn_vector fields that enables disk-based vector search in OpenSearch, allowing searches to run in lower-memory environments. This is achieved using a two-phase query approach, illustrated in the following diagram.
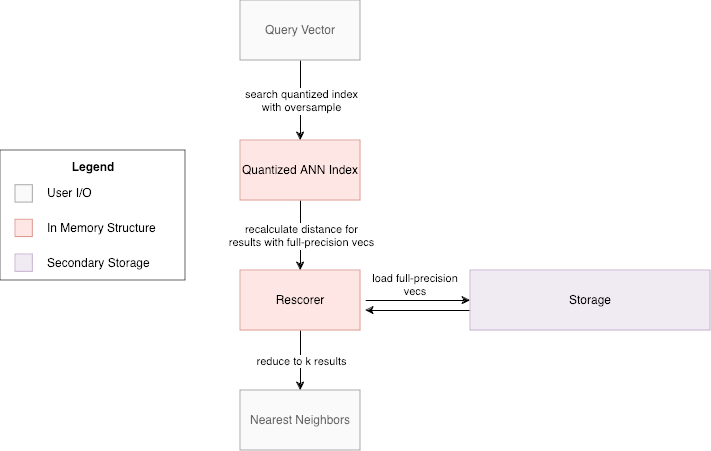
First, during ingestion, we build indexes using configurable quantization mechanisms and store the full-precision vectors on disk. The quantized indexes, which reside fully in memory during search, require significantly less memory due to compression.
During search, we first query the quantized indexes to retrieve more than k candidate results. Then we lazily load the full-precision vectors of these candidates into memory and recompute the distance to the query. This reordering step ensures accuracy, and we return only the top k results.
Empirically, this two-phase approach has demonstrated the ability to produce high-recall results across a variety of quantization techniques.
Introducing online binary quantization
As part of this feature, we also expanded our quantization support. Previously, achieving ≥8x compression in OpenSearch required using product quantization. While effective, product quantization requires a training step before ingestion can begin and requires users to manage their models.
In 2.17, we introduced several new online quantization techniques for 8x, 16x, and 32x compression—no pretraining needed. You can begin ingestion immediately without additional model preparation. This simplifies the process and reduces overhead. Take a look at this technical deep dive to learn how we developed these capabilities.
Consider the following 8-dimensional vectors of 32-bit floating-point numbers:
v1 = [0.56, 0.85, 0.53, 0.25, 0.46, 0.01, 0.63, 0.73]
v2 = [-0.99, -0.79, 0.23, -0.62, 0.87, -0.06, -0.24, -0.75]
v3 = [-0.15, 0.17, 0.10, 0.46, -0.79, -0.31, 0.36, -1.00]
In order to quantize them, we perform the following steps.
1. Calculate mean per dimension
The mean for each dimension j is calculated using the following formula:
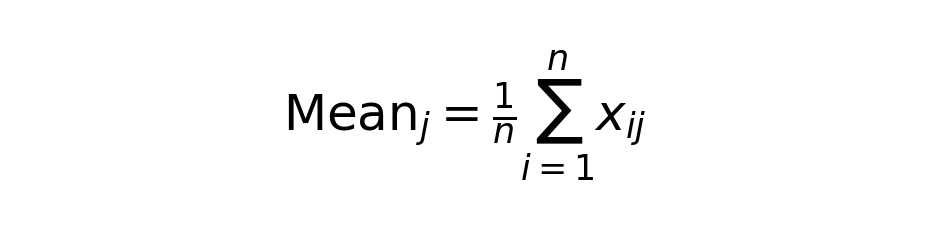
The preceding set of vectors produces the following calculated mean:
Mean = [-0.19, 0.08, 0.29, 0.03, 0.18, -0.12, 0.25, -0.34]
2. Quantization of a new vector
The quantization rule for each dimension j of a vector is given by the following logic:
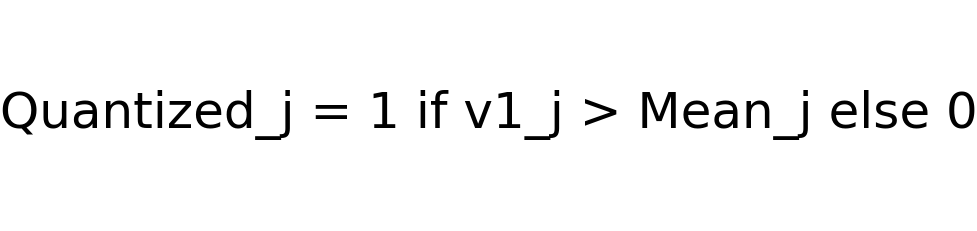
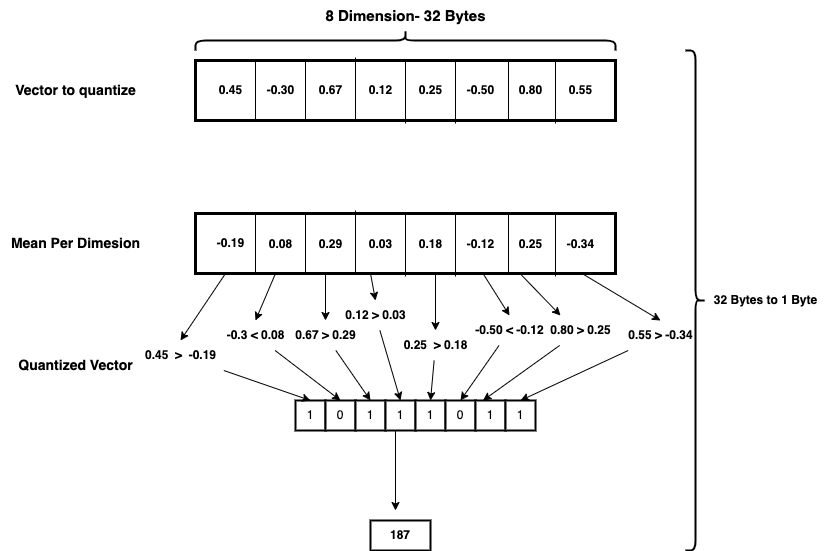
Consider a new vector:
v_new = [0.45, -0.30, 0.67, 0.12, 0.25, -0.50, 0.80, 0.55]
To quantize this vector, we compare each dimension to the mean value. When a dimension exceeds the mean, we convert it to 1; otherwise, we convert it to 0, as shown in the following diagram.
Try disk-based vector search
To set up disk-based vector search, simply set the mode to on_disk in the index mappings. This parameter automatically configures a low-memory setting with rescoring enabled:
PUT my-vector-index
{
"settings" : {
"index.knn": true
},
"mappings": {
"properties": {
"my_vector_field": {
"type": "knn_vector",
"dimension": 8,
"space_type": "innerproduct",
"mode": "on_disk"
}
}
}
}
To tune the quantization, you can specify the compression_level in the mapping. By default for on_disk mode, it is 32x:
PUT my-vector-index
{
"settings" : {
"index.knn": true
},
"mappings": {
"properties": {
"my_vector_field": {
"type": "knn_vector",
"dimension": 8,
"space_type": "innerproduct",
"mode": "on_disk",
"compression_level": "16x"
}
}
}
}
At search time, if mode is set to on_disk, OpenSearch automatically applies a two-phase search process:
GET my-vector-index/_search
{
"query": {
"knn": {
"my_vector_field": {
"vector": [1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
"k": 5
}
}
}
}
When you use on_disk mode, OpenSearch configures an oversample factor to return more than k results from the quantized index search. You can override this default setting by specifying an oversample_factor in the query body:
GET my-vector-index/_search
{
"query": {
"knn": {
"my_vector_field": {
"vector": [1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
"k": 5,
"rescore": {
"oversample_factor": 10.0
}
}
}
}
}
For more information, see Disk-based vector search.
Experiments
To evaluate the performance of disk-based vector search, we conducted several experiments using various dataset sizes and configurations.
One million vector tests
We ran several different tests on a single-node OpenSearch cluster for datasets containing between 1 and 10 million vectors.
| Name | Space type | Normalized | Dimension | Index vector count | Notes |
|---|---|---|---|---|---|
sift |
l2 |
No | 128 | 1,000,000 | Classic scale-invariant feature transform (SIFT) image descriptor dataset. |
minillm-msmarco |
l2 |
Yes | 384 | 1,000,000 | Used minillm to encode a sample of ms-marco. |
mpnet-msmarco |
l2 |
Yes | 768 | 1,000,000 | Used mpnet to encode a sample of ms-marco. |
mxbai-msmarco |
cosine |
Yes | 1,024 | 1,000,000 | Used mxbai to encode a sample of ms-marco. |
tasb-msmarco |
ip |
No | 768 | 1,000,000 | Used tasb to encode a sample of ms-marco. |
e5small-msmarco |
l2 |
Yes | 384 | 8,841,823 | Used e5small to encode a larger sample of ms-marco. |
sNowflake-msmarco |
l2 |
Yes | 768 | 8,841,823 | Used snowflake-arctic-embed-m to encode a larger sample of ms-marco. |
clip-flickr |
l2 |
No | 512 | 6,637,685 | Used the clip model to encode a random sample of images from Flickr. |
We conducted experiments comparing in_memory and on_disk modes using 1x, 2x, 4x, 8x, 16x, and 32x compression levels. Key testing parameters included the following:
on_diskmode: Includes a rescoring stagein_memorymode: Does not include a rescoring stage- Hardware configuration:
in_memorytests: Amazon Elastic Compute Cloud (Amazon EC2) r6g.4xlarge instanceson_disktests: Amazon EC2 r6gd.4xlarge instances with an attached solid-state drive (SSD)—as opposed to Amazon Elastic Block Store (Amazon EBS) storage
- Resource controls: Used Docker to manage OpenSearch’s memory and CPU allocation
We obtained the following results, comparing recall to compression level.
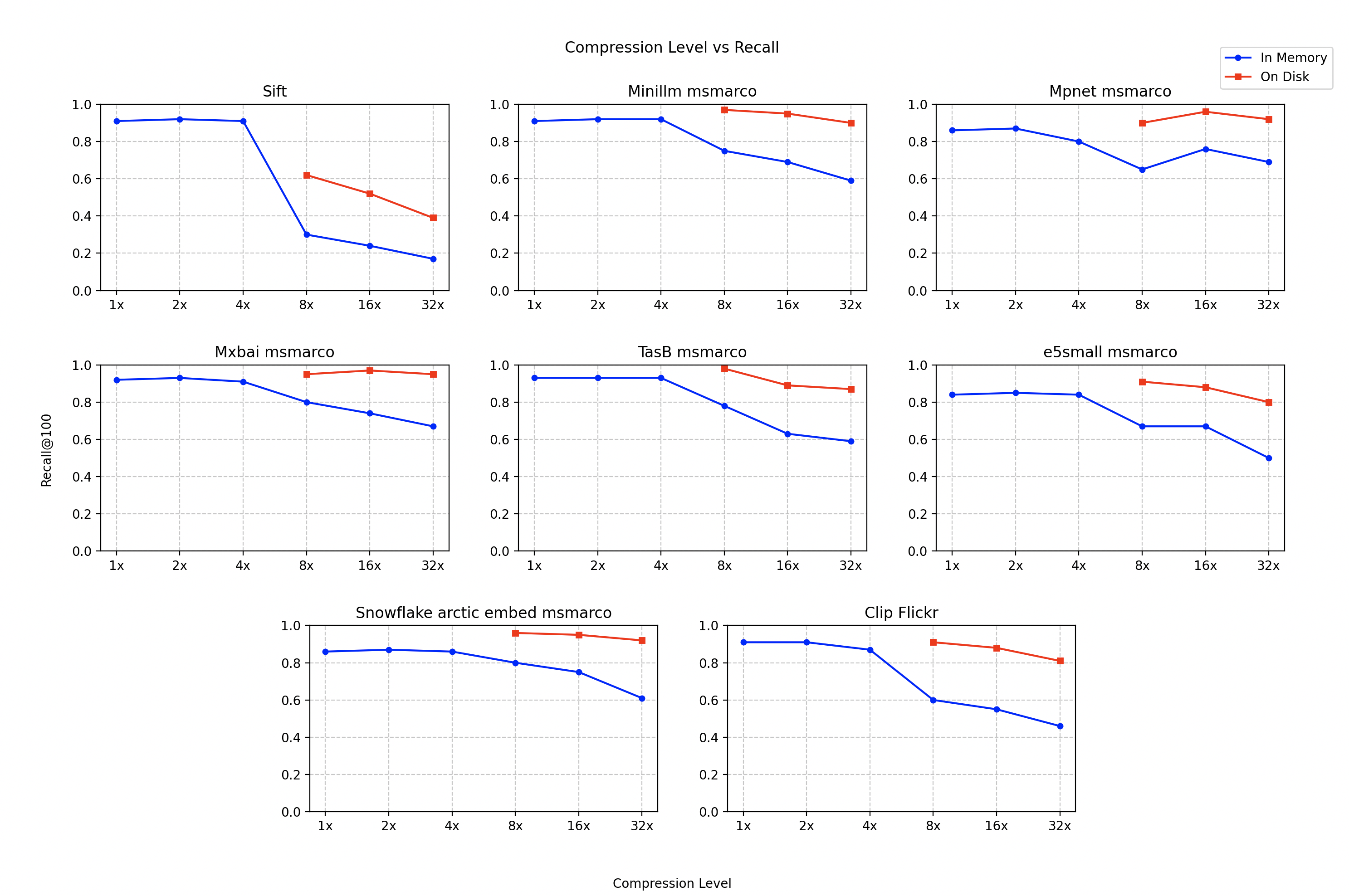
The results show that combining quantization with full-precision rescoring can significantly improve recall while maintaining reasonable latency in low-memory environments. However, performance varies by dataset. For example, while this approach improves the performance of the sift dataset, the recall remains relatively low. We recommend testing using your specific dataset to determine the optimal configuration.
Large-scale tests
In addition to the smaller-scale tests, we also ran a test on a larger dataset, MS MARCO 2.1 encoded with the Cohere v3 model. We set up several different tests to showcase how this disk-based vector search compares to in_memory vector search at 8x, 16x, and 32x compression levels. We ran these tests using the following configuration.
| Dataset | MS MARCO 2.1 encoded with the Cohere v3 model |
| Dimension | 1,024 |
| Normalized | Yes |
| Space type | Cosine (inner product over normalized data) |
| Index vectors | 113M |
We tested four different cluster configurations using the opensearch-cluster-cdk with OpenSearch 2.18. We selected the cluster and index configuration to follow production recommendations. For example, we configured replica shards and dedicated cluster manager nodes. In addition, we targeted a shard count that provides 2 to 3 vCPUs per shard. The following table presents the configurations for these tests.
| Name | Data node count | Data node type | Data node disk size | Data node disk type | JVM size | Primary shard count | Replica shards | Compression level |
|---|---|---|---|---|---|---|---|---|
in_memory |
8 | r6g.8xlarge | 300 | EBS | 32 | 40 | 1 | 1x |
on_disk_8x |
10 | r6gd.2xlarge | 474 | Instance | 32 | 15 | 1 | 8x |
on_disk_16x |
6 | r6gd.2xlarge | 474 | Instance | 32 | 9 | 1 | 16x |
on_disk_32x |
4 | r6gd.2xlarge | 474 | Instance | 32 | 6 | 1 | 32x |
In the table, note that clusters with higher compression levels use significantly fewer resources than those without compression.
To optimize performance in our tests, we made these additional adjustments:
- Retrieved IDs from
doc_valuesto reduce fetch time - Disabled
_sourcestorage
We ran all tests using OpenSearch Benchmark vector search workloads, following this procedure:
- Ingest the dataset.
- Force merge the index to 5 segments per shard.
- Run warm-up queries to load the index into memory.
- Run the single-client latency test.
- Run the multi-client throughput test.
- Repeat steps 4 and 5 with disk-based rescoring disabled to measure performance on a compressed index without rescoring.
We obtained the following large-scale test results.
| Metric/configuration | in-memory |
on_disk_8x |
in_memory_8x |
on_disk_16x |
in_memory_16x |
on_disk_32x |
in_memory_32x |
|---|---|---|---|---|---|---|---|
| recall@100 (ratio) | 0.95 | 0.98 | 0.98 | 0.97 | 0.96 | 0.94 | 0.95 |
| 1-client p90 search latency (ms) | 24.02 | 96.31 | 28.90 | 108.05 | 29.79 | 104.421 | 47.2906 |
| 1-client mean throughput (QPS) | 40.64 | 11.03 | 42.33 | 10.06 | 43.95 | 10.65 | 31.83 |
| 4-client p90 search latency (ms) | 25.82 | 97.19 | 20.40 | 220.19 | 18.09 | 244.52 | 46.13 |
| 4-client mean throughput (QPS) | 162.80 | 45.86 | 204.62 | 25.80 | 193.27 | 25.28 | 146.77 |
| 8-client p90 search latency (ms) | 27.69 | 95.05 | 30.88 | 414.20 | 27.94 | 429.79 | 25.07 |
| 8-client mean throughput (QPS) | 306.70 | 95.22 | 305.86 | 26.34 | 343.95 | 25.75 | 376.60 |
Interestingly, for this dataset, the on-disk approach with rescoring produces similar recall to the in-memory approach without rescoring, but the in-memory approach is substantially faster. This is most likely because the Cohere v3 model has been optimized to work very well with binary quantized data (see this blog post).
Learnings
Our testing shows that the two-phase approximate nearest neighbor approach performs effectively in low-memory environments, though results vary significantly by dataset. When running your own experiments, we recommend testing with the index.knn.disk.vector.shard_level_rescoring_disabled setting both enabled and disabled to measure the performance benefit for your use case. Additionally, with disk-based search, ensure that your secondary storage is optimized for high read traffic—we found that SSDs generally provide the best results.
What’s next?
We have many new and exciting features coming for vector search in OpenSearch. In future versions, we’ll focus on improving quantization performance for all datasets, eliminating the need for fine-tuning. Follow our GitHub repo for continued improvements in both performance and functionality. As always, we welcome and appreciate your contributions and feature requests!






